



Attenzione: tutte le pagine prevedono un titolo iniziale di livello 1. Per una lettura ordinata, a ogni nuova pagina è preferibile accedere al titolo.
Numeri razionali rappresentati come numeri decimali o frazioni
 Esiste contrapposizione tra frazioni e numeri decimali?
Esiste contrapposizione tra frazioni e numeri decimali?
Numeri razionali rappresentati come numeri decimali o frazioni
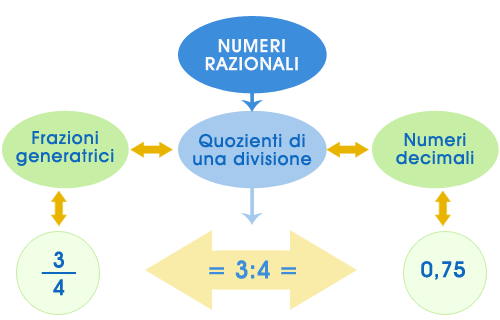
 classe di equivalenza, attraverso la frazione ridotta ai minimi termini, sia tramite la scrittura decimale cioè quella che esprime anche quantità inferiori alle unità (decimi, centesimi, millesimi e così via).
classe di equivalenza, attraverso la frazione ridotta ai minimi termini, sia tramite la scrittura decimale cioè quella che esprime anche quantità inferiori alle unità (decimi, centesimi, millesimi e così via). Ogni frazione, in quanto quoziente di una divisione, genera:
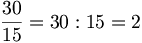
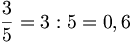
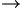 il resto della divisione è sempre
il resto della divisione è sempre 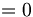
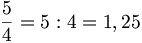
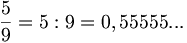
 il resto della divisione è sempre uno stesso numero
il resto della divisione è sempre uno stesso numero 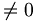
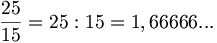
Numeri razionali rappresentati come numeri decimali o frazioni
Un numero decimale limitato o finito è costituito da una parte intera e da cifre decimali, in numero definito, separate dalla virgola. La sua frazione generatrice è detta frazione decimale.
Per esempio 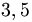 è un decimale limitato e
è un decimale limitato e 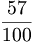 è una frazione decimale.
è una frazione decimale.
La frazione generatrice di un numero decimale limitato è una frazione decimale, ovvero una frazione il cui denominatore è 10 o una potenza di 10.
Un numero decimale illimitato periodico è costituito da una parte intera e da cifre decimali, almeno alcune delle quali ripetute indefinitamente, che costituiscono il periodo.
Se il periodo inizia subito dopo la virgola il numero decimale illimitato è detto periodico semplice. Se, invece, il periodo non inizia subito dopo la virgola ma è preceduto da una o più cifre, definite antiperiodo, allora il numero si dice periodico misto.
Ad esempio 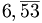 è un periodico semplice e
è un periodico semplice e 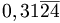 è un periodico misto.
è un periodico misto.
La frazione generatrice di un numero decimale illimitato periodico è una frazione generica, ovvero non decimale.
Numeri razionali rappresentati come numeri decimali o frazioni
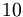 .
.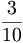 è una frazione decimale perché ha al denominatore
è una frazione decimale perché ha al denominatore 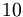
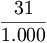 è una frazione decimale perché ha al denominatore
è una frazione decimale perché ha al denominatore 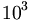 , una potenza di dieci
, una potenza di dieci
Data una frazione decimale si ottiene facilmente il numero decimale corrispondente scrivendone il numeratore e separando con la virgola tante cifre decimali quante ne indica l'esponente della potenza di 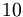 al denominatore.
al denominatore.
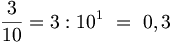 l'esponente è 1
l'esponente è 1 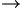 1 cifra decimale
1 cifra decimale
 l'esponente è 3
l'esponente è 3  3 cifre decimali
3 cifre decimali
Analogamente da un numero decimale limitato si ricava la corrispondente frazione decimale, scrivendo al numeratore della frazione tutto il numero senza la virgola e al denominatore la potenza di 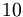 che ha tanti zeri quante sono le cifre decimali.
che ha tanti zeri quante sono le cifre decimali.
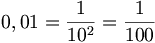 2 sono le cifre decimali
2 sono le cifre decimali  l'esponente è 2
l'esponente è 2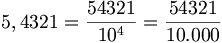 4 sono le cifre decimali
4 sono le cifre decimali 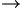 l'esponente è 4
l'esponente è 4
Sono riconducibili a frazioni decimali tutte quelle il cui denominatore è scomponibile nei numeri 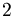 e/o
e/o 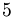 .
.
Esempio: 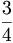 ,
, 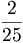 ,
, 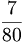 .
.
Un  semplice metodo consente di ottenere da una frazione ordinaria quella decimale equivalente.
semplice metodo consente di ottenere da una frazione ordinaria quella decimale equivalente.
Numeri razionali rappresentati come numeri decimali o frazioni
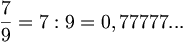
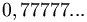 si indica
si indica 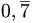 oppure
oppure 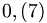
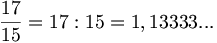
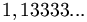 si indica
si indica 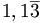 oppure
oppure 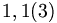
Solo le cifre del periodo si scrivono con sopra un trattino o in parentesi tonda.
Sono frazioni generatrici di numeri periodici semplici tutte quelle il cui denominatore non è mai scomponibile nei numeri 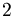 e/o
e/o 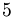 .
.
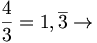 la scomposizione di
la scomposizione di 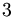 è
è 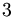
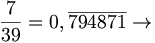 la scomposizione di
la scomposizione di 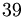 è
è 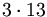
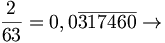 la scomposizione di
la scomposizione di 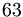 è
è 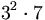
Sono frazioni generatrici di numeri periodici misti tutte quelle il cui denominatore è scomponibile anche nei numeri 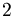 e/o
e/o 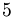 .
.
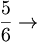 la scomposizione di
la scomposizione di 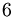 è
è 
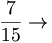 la scomposizione di
la scomposizione di  è
è 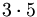
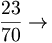 la scomposizione di
la scomposizione di 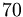 è
è 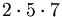
Numeri razionali rappresentati come numeri decimali o frazioni
Esempio: 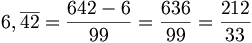
La frazione generatrice di un numero decimale periodico misto si ottiene scrivendo
Esempio: 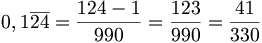
Un  caso particolare si ha se il periodo è uguale a 9.
caso particolare si ha se il periodo è uguale a 9.
Numeri razionali rappresentati come numeri decimali o frazioni
Frazioni e numeri decimali costituiscono differenti modalità di rappresentare
i numeri razionali.
Parole nuove
Numeri decimali limitati
Numeri decimali periodici
Numeri decimali periodici semplici
Numeri decimali periodici misti
Frazioni decimali
Il termine ordinario indica ciò che sta nell'ordine delle cose, che si fa regolarmente, che avviene di solito.
Sinonimi: Consueto, Comune
Etimologia
Ordinario deriva dal latino ordo e letteralmente significa "ordine"
Principali funzioni:
 Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Fine dell'approfondimento. Per riascoltarlo torna al titolo.
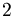 e/o
e/o 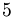
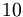 più vicina, moltiplicandolo per i fattori mancanti
più vicina, moltiplicandolo per i fattori mancanti
Esempio 1)
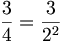
Poiché la scomposizione del denominatore contiene solo il fattore 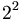 , la potenza di
, la potenza di 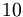 più vicina è
più vicina è 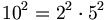 ; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per il fattore mancante
; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per il fattore mancante 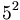 ottenendo
ottenendo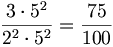
Esempio 2)
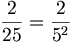
In questo caso la scomposizione del denominatore contiene solo il fattore 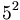 ; la potenza di
; la potenza di 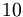 più vicina è ancora
più vicina è ancora 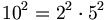 ; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per
; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per 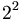 ottenendo
ottenendo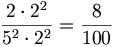
Esempio 3)
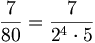
In questo caso la scomposizione del denominatore contiene sia il fattore 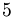 sia
sia 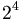 ; la potenza di
; la potenza di 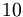 più vicina è
più vicina è 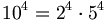 ; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per
; pertanto occorre moltiplicare tanto il numeratore quanto il denominatore per 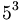 ottenendo
ottenendo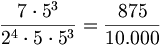
Principali funzioni:
 Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Un numero decimale periodico semplice con periodo 9 genera una frazione apparente.
Esempio: 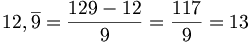
Una semplice regola pratica permette di ricavare il numero intero corrispondente alla frazione apparente generata: basta aumentare di una unità la cifra della parte intera precedente il periodo.
Infatti 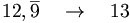
Un numero decimale periodico misto con periodo 9 genera una frazione decimale.
Esempio: 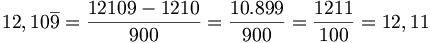
Anche in questo caso una semplice regola pratica permette di ricavare il numero decimale limitato corrispondente alla frazione generata: basta aumentare di una unità l'ultima cifra dell'antiperiodo.
Infatti 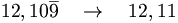
Principali funzioni:
 Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Si dice classe di equivalenza di frazioni un insieme di infinite frazioni equivalenti.
La frazione ridotta ai minimi termini, per comodità, è scelta come rappresentante della classe.
Due frazioni  e
e 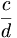 si sicono equivalenti se
si sicono equivalenti se 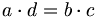 .
.
Da una frazione si ottengono frazioni equivalenti moltiplicando numeratore e denominatore per lo stesso numero diverso da zero.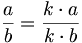
oppure dividendo entrambi per un divisore comune: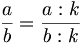
Principali funzioni:
 Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Fine dell'approfondimento. Per riascoltarlo torna al titolo.
Questo corso ha una struttura sequenziale che permette di seguire facilmente il flusso di informazioni multimediali (testi, immagini, filmati, animazioni) e prove di verifica con pochissimi comandi.

 I pulsanti "Indietro" e "Avanti" e consentono di scorrere le pagine. Se il pulsante "Avanti" non è visibile, a meno che non si tratti dell'ultima pagina, nella schermata ci sono certamente indicazioni su come proseguire.
I pulsanti "Indietro" e "Avanti" e consentono di scorrere le pagine. Se il pulsante "Avanti" non è visibile, a meno che non si tratti dell'ultima pagina, nella schermata ci sono certamente indicazioni su come proseguire. e
e  .
.
 Il pulsante "Home" consente di raggiungere direttamente la pagina iniziale ("home page"), che contiene una scheda sintetica del corso.
Il pulsante "Home" consente di raggiungere direttamente la pagina iniziale ("home page"), che contiene una scheda sintetica del corso.
 Il pulsante "Indice" consente di raggiungere direttamente l'indice del corso. Da qui può essere possibile accedere alle diverse pagine.
Il pulsante "Indice" consente di raggiungere direttamente l'indice del corso. Da qui può essere possibile accedere alle diverse pagine. .
.
 Il pulsante "Help" consente di accedere alla pagina delle istruzioni (questa!), che contiene indicazioni sulle diverse funzioni e sui comandi.
Il pulsante "Help" consente di accedere alla pagina delle istruzioni (questa!), che contiene indicazioni sulle diverse funzioni e sui comandi.
 Il pulsante "Informazioni" consente di accedere alla pagina con informazioni sugli autori. Equivale ai titoli di coda di un film (credits).
Il pulsante "Informazioni" consente di accedere alla pagina con informazioni sugli autori. Equivale ai titoli di coda di un film (credits).
 Il pulsante "Torna" serve a tornare indietro. Il suo funzionamento è differente a seconda dei casi:
Il pulsante "Torna" serve a tornare indietro. Il suo funzionamento è differente a seconda dei casi:
 Il pulsante "Verifica" permette di controllare l'esito di un test e di assegnare i relativi punteggi.
Il pulsante "Verifica" permette di controllare l'esito di un test e di assegnare i relativi punteggi.
 Il pulsante "Studia" (o "Vai a vedere") permette di collegare un test alle pagine che contengono le necessarie conoscenze teoriche.
Il pulsante "Studia" (o "Vai a vedere") permette di collegare un test alle pagine che contengono le necessarie conoscenze teoriche. Il pulsante "Soluzione" permette di conoscere le soluzioni dei test.
Il pulsante "Soluzione" permette di conoscere le soluzioni dei test. o
o  .
.

 I pulsanti "Ingrandisci" e "Rimpicciolisci" permettono di modificare a piacere le dimensioni dei caratteri del testo.
I pulsanti "Ingrandisci" e "Rimpicciolisci" permettono di modificare a piacere le dimensioni dei caratteri del testo.
 Il pulsante "Zoom" permette di scegliere tra due possibili dimensioni della schermata, per adattarle a quelle del monitor.
Il pulsante "Zoom" permette di scegliere tra due possibili dimensioni della schermata, per adattarle a quelle del monitor.

 Il pulsanti "Attiva/disattiva audio, video e animazioni" permettono di attivare o disabilitare tutti i contenuti multimediali: suoni, filmati, animazioni Flash, ecc.
Il pulsanti "Attiva/disattiva audio, video e animazioni" permettono di attivare o disabilitare tutti i contenuti multimediali: suoni, filmati, animazioni Flash, ecc.
Principali funzioni:
 Fine dell'help. Per riascoltarlo torna al titolo.
Fine dell'help. Per riascoltarlo torna al titolo.
Produzione editoriale
Garamond Editoria e Formazione - Roma
Consulenza didattica
Vindice Deplano
Ideazione e produzione storyboard e testi
Rita Bartole
Coordinamento disciplinare
Licia Cianfriglia
Redazione
Paola Ricci (coordinamento), Claudio Bafera, Mimma Basile, Brunella Pellegrini, Martina Quadrino, Stefano Tura
Progettazione e sviluppo editor LO
Francesco Leonetti
Progettazione e realizzazione grafica
Cristiana Giovannini
Sviluppo animazioni
Andrea Blasio, Gaetano Ermito, Glaux srl
Audio, musiche ed effetti sonori
Luca De Carlo, Gio Gio' Rapattoni (voce)
Comunicazione
Chiara Calzavara

"Creative Commons - Attribuzione, Non Commerciale, Condividi allo stesso modo 2.5 Italia"
Questo learning object è distribuito da Garamond secondo la Licenza Creative Commons che consente di riprodurlo e ridistribuirlo a condizione che siano rispettate queste condizioni:



Attribuzione. Si deve attribuire la paternità dell'opera nei modi indicati dall'autore o da chi ha dato l'opera in licenza.
Non commerciale. Non si può usare quest'opera per fini commerciali.
Condividi allo stesso modo. Se si altera o si trasforma quest'opera, o se la si usa per crearne un'altra, si può distribuire l'opera risultante solo con una licenza identica a questa.
Il Commons Deed della presente licenza "Creative Commons - Attribuzione, Non Commerciale, Condividi allo stesso modo 2.5 Italia" è pubblicato sul sito web: http://creativecommons.org/licenses/by-nc-sa/2.5/it/
La licenza integrale è pubblicata sul sito web http://creativecommons.org/licenses/by-nc-sa/2.5/it/legalcode
Principali funzioni:
 Fine dei credits. Per riascoltarli torna al titolo.
Fine dei credits. Per riascoltarli torna al titolo.















Principali funzioni:
 Fine dell'indice generale. Per riascoltarlo torna al titolo.
Fine dell'indice generale. Per riascoltarlo torna al titolo.